3. 题目实践

下面我们来看力扣第 797 题「 所有可能路径 」，函数签名如下：

List<List<Integer>> allPathsSourceTarget(int[][] graph);

题目输入一幅有向无环图，这个图包含 n 个节点，标号为 0, 1, 2,..., n - 1，请你计算所有从节点 0 到节点 n - 1 的路径。

输入的这个 graph 其实就是「邻接表」表示的一幅图，graph[i] 存储这节点 i 的所有邻居节点。

比如输入 graph = [[1,2],[3],[3],[]]，就代表下面这幅图：

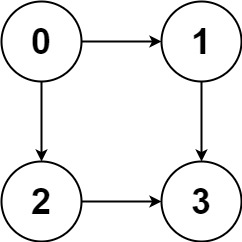
算法应该返回 [[0,1,3],[0,2,3]]，即 0 到 3 的所有路径。

解法很简单，以 0 为起点遍历图，同时记录遍历过的路径，当遍历到终点时将路径记录下来即可。

既然输入的图是无环的，我们就不需要 visited 数组辅助了，直接套用图的遍历框架：

class Solution {
    // 记录所有路径
    List<List<Integer>> res = new LinkedList<>();
 
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        // 维护递归过程中经过的路径
        LinkedList<Integer> path = new LinkedList<>();
        traverse(graph, 0, path);
        return res;
    }
 
    /* 图的遍历框架 */
    void traverse(int[][] graph, int s, LinkedList<Integer> path) {
        // 添加节点 s 到路径
        path.addLast(s);
 
        int n = graph.length;
        if (s == n - 1) {
            // 到达终点
            res.add(new LinkedList<>(path));
            // 可以在这直接 return，但要 removeLast 正确维护 path
            // path.removeLast();
            // return;
            // 不 return 也可以，因为图中不包含环，不会出现无限递归
        }
 
        // 递归每个相邻节点
        for (int v : graph[s]) {
            traverse(graph, v, path);
        }
 
        // 从路径移出节点 s
        path.removeLast();
    }
}
 

这道题就这样解决了，注意 Java 的语言特性，因为 Java 函数参数传的是对象引用，所以向 res 中添加 path 时需要拷贝一个新的列表，否则最终 res 中的列表都是空的。

最后总结一下，图的存储方式主要有邻接表和邻接矩阵，无论什么花里胡哨的图，都可以用这两种方式存储。

在笔试中，最常考的算法是图的遍历，和多叉树的遍历框架是非常类似的。

当然，图还会有很多其他的有趣算法，比如 [二分图判定]，[环检测和拓扑排序]（编译器循环引用检测就是类似的算法），[最小生成树]，[Dijkstra 最短路径算法] 等等，有兴趣的读者可以去看看，本文就到这了。

附上大佬的可视化算法： 图论基础及遍历算法 | labuladong 的算法笔记