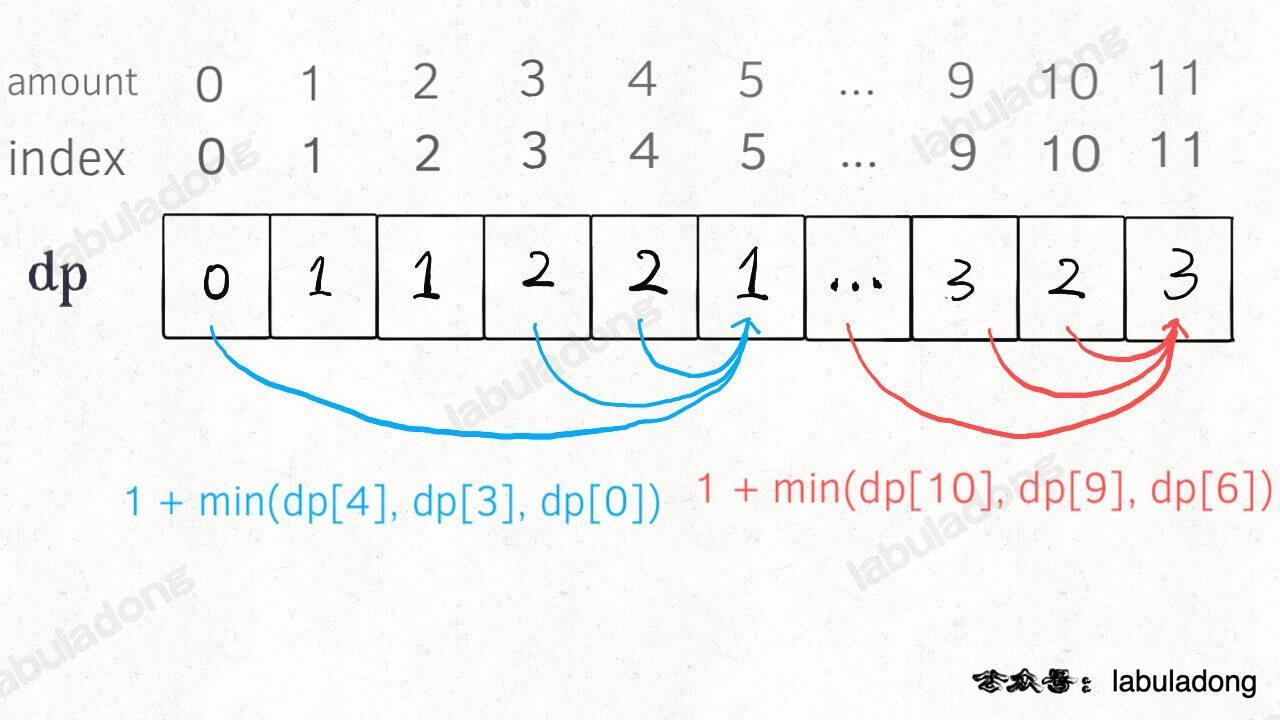
这是力扣第 322 题零钱兑换
给你 k 种面值的硬币,面值分别为 c1, c2 ... ck,每种硬币的数量无限,再给一个总金额 amount,问你最少需要几枚硬币凑出这个金额,如果不可能凑出,算法返回 -1 。算法的函数签名如下:
// coins 中是可选硬币面值,amount 是目标金额
int coinChange(int[] coins, int amount);
比如说 k = 3,面值分别为 1,2,5,总金额 amount = 11。那么最少需要 3 枚硬币凑出,即 11 = 5 + 5 + 1。
你认为计算机应该如何解决这个问题?显然,就是把所有可能的凑硬币方法都穷举出来,然后找找看最少需要多少枚硬币。
1、暴力递归
首先,这个问题是动态规划问题,因为它具有「最优子结构」的。要符合「最优子结构」,子问题间必须互相独立。啥叫相互独立?你肯定不想看数学证明,我用一个直观的例子来讲解。
比如说,假设你考试,每门科目的成绩都是互相独立的。你的原问题是考出最高的总成绩,那么你的子问题就是要把语文考到最高,数学考到最高…… 为了每门课考到最高,你要把每门课相应的选择题分数拿到最高,填空题分数拿到最高…… 当然,最终就是你每门课都是满分,这就是最高的总成绩。
得到了正确的结果:最高的总成绩就是总分。因为这个过程符合最优子结构,「每门科目考到最高」这些子问题是互相独立,互不干扰的。
但是,如果加一个条件:你的语文成绩和数学成绩会互相制约,不能同时达到满分,数学分数高,语文分数就会降低,反之亦然。
这样的话,显然你能考到的最高总成绩就达不到总分了,按刚才那个思路就会得到错误的结果。因为「每门科目考到最高」的子问题并不独立,语文数学成绩户互相影响,无法同时最优,所以最优子结构被破坏。
重点:
回到凑零钱问题,为什么说它符合最优子结构呢?假设你有面值为 1, 2, 5 的硬币,你想求 amount = 11 时的最少硬币数(原问题),如果你知道凑出 amount = 10, 9, 6 的最少硬币数(子问题),你只需要把子问题的答案加一(再选一枚面值为 1, 2, 5 的硬币),求个最小值,就是原问题的答案。因为硬币的数量是没有限制的,所以子问题之间没有相互制,是互相独立的。
关于最优子结构的问题,后文 动态规划答疑篇 还会再举例探讨。
那么,既然知道了这是个动态规划问题,就要思考如何列出正确的状态转移方程?
1、确定 base case,这个很简单,显然目标金额 amount 为 0 时算法返回 0,因为不需要任何硬币就已经凑出目标金额了。
2、确定「状态」,也就是原问题和子问题中会变化的变量。由于硬币数量无限,硬币的面额也是题目给定的,只有目标金额会不断地向 base case 靠近,所以唯一的「状态」就是目标金额 amount。
3、确定「选择」,也就是导致「状态」产生变化的行为。目标金额为什么变化呢,因为你在选择硬币,你每选择一枚硬币,就相当于减少了目标金额。所以说所有硬币的面值,就是你的「选择」。
4、明确 dp 函数/数组的定义。我们这里讲的是自顶向下的解法,所以会有一个递归的 dp 函数,一般来说函数的参数就是状态转移中会变化的量,也就是上面说到的「状态」;函数的返回值就是题目要求我们计算的量。就本题来说,状态只有一个,即「目标金额」,题目要求我们计算凑出目标金额所需的最少硬币数量。
所以我们可以这样定义 dp 函数:dp(n) 表示,输入一个目标金额 n,返回凑出目标金额 n 所需的最少硬币数量。
搞清楚上面这几个关键点,解法的伪码就可以写出来了:
// 伪码框架
int coinChange(int[] coins, int amount) {
// 题目要求的最终结果是 dp(amount)
return dp(coins, amount)
}
// 定义:要凑出金额 n,至少要 dp(coins, n) 个硬币
int dp(int[] coins, int n) {
// 做选择,选择需要硬币最少的那个结果
for (int coin : coins) {
res = min(res, 1 + dp(coins, n - coin))
}
return res
}根据伪码,我们加上 base case 即可得到最终的答案。显然目标金额为 0 时,所需硬币数量为 0;当目标金额小于 0 时,无解,返回 -1:
int coinChange(int[] coins, int amount) {
// 题目要求的最终结果是 dp(amount)
return dp(coins, amount)
}
// 定义:要凑出金额 n,至少要 dp(coins, n) 个硬币
int dp(int[] coins, int amount) {
// base case
if (amount == 0) return 0;
if (amount < 0) return -1;
int res = Integer.MAX_VALUE;
for (int coin : coins) {
// 计算子问题的结果
int subProblem = dp(coins, amount - coin);
// 子问题无解则跳过
if (subProblem == -1) continue;
// 在子问题中选择最优解,然后加一
res = Math.min(res, subProblem + 1);
}
return res == Integer.MAX_VALUE ? -1 : res;
}这里 coinChange 和 dp 函数的签名完全一样,所以理论上不需要额外写一个 dp 函数。但为了后文讲解方便,这里还是另写一个 dp 函数来实现主要逻辑。
另外,我经常看到有人问,子问题的结果为什么要加 1(
subProblem + 1),而不是加硬币金额之类的。我这里统一提示一下,动态规划问题的关键是dp函数/数组的定义,你这个函数的返回值代表什么?你回过头去搞清楚这一点,然后就知道为什么要给子问题的返回值加 1 了。
至此,状态转移方程其实已经完成了,以上算法已经是暴力解法了,以上代码的数学形式就是状态转移方程:
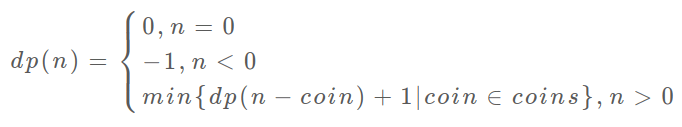
至此,这个问题其实就解决了,只不过需要消除一下重叠子问题,比如 amount = 11, coins = {1,2,5} 时画出递归树看看:
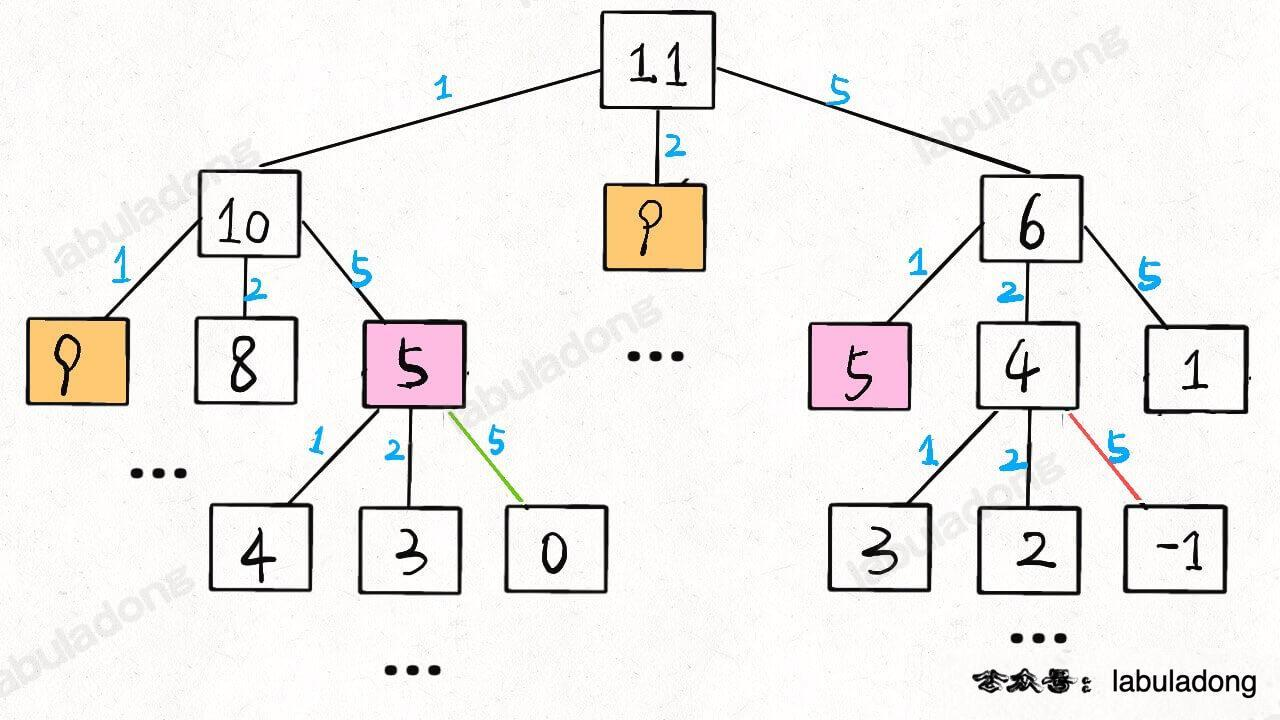
递归算法的时间复杂度分析:子问题总数 x 解决每个子问题所需的时间。
子问题总数为递归树的节点个数,但算法会进行剪枝,剪枝的时机和题目给定的具体硬币面额有关,所以可以想象,这棵树生长的并不规则,确切算出树上有多少节点是比较困难的。对于这种情况,我们一般的做法是按照最坏的情况估算一个时间复杂度的上界。
假设目标金额为 n,给定的硬币个数为 k,那么递归树最坏情况下高度为 n(全用面额为 1 的硬币),然后再假设这是一棵满 k 叉树,则节点的总数在 k^n 这个数量级。
接下来看每个子问题的复杂度,由于每次递归包含一个 for 循环,复杂度为 O(k),相乘得到总时间复杂度为 O(k^n),指数级别。
2、带备忘录的递归
类似之前斐波那契数列的例子,只需要稍加修改,就可以通过备忘录消除子问题:
class Solution {
int[] memo;
int coinChange(int[] coins, int amount) {
memo = new int[amount + 1];
// 备忘录初始化为一个不会被取到的特殊值,代表还未被计算
Arrays.fill(memo, -666);
return dp(coins, amount);
}
int dp(int[] coins, int amount) {
if (amount == 0) return 0;
if (amount < 0) return -1;
// 查备忘录,防止重复计算
if (memo[amount] != -666)
return memo[amount];
int res = Integer.MAX_VALUE;
for (int coin : coins) {
// 计算子问题的结果
int subProblem = dp(coins, amount - coin);
// 子问题无解则跳过
if (subProblem == -1) continue;
// 在子问题中选择最优解,然后加一
res = Math.min(res, subProblem + 1);
}
// 把计算结果存入备忘录
memo[amount] = (res == Integer.MAX_VALUE) ? -1 : res;
return memo[amount];
}
}https://labuladong.gitee.io/algo/di-ling-zh-bfe1b/dong-tai-g-1e688/#div_coin-change
不画图了,很显然「备忘录」大大减小了子问题数目,完全消除了子问题的冗余,所以子问题总数不会超过金额数 n,即子问题数目为 O(n)。处理一个子问题的时间不变,仍是 O(k),所以总的时间复杂度是 O(kn)。
3、dp 数组的迭代解法
当然,我们也可以自底向上使用 dp table 来消除重叠子问题,关于「状态」「选择」和 base case 与之前没有区别,dp 数组的定义和刚才 dp 函数类似,也是把「状态」,也就是目标金额作为变量。不过 dp 函数体现在函数参数,而 dp 数组体现在数组索引:
dp 数组的定义:当目标金额为 i 时,至少需要 dp[i] 枚硬币凑出。
根据我们文章开头给出的动态规划代码框架可以写出如下解法:
int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
// 数组大小为 amount + 1,初始值也为 amount + 1
Arrays.fill(dp, amount + 1);
// base case
dp[0] = 0;
// 外层 for 循环在遍历所有状态的所有取值
for (int i = 0; i < dp.length; i++) {
// 内层 for 循环在求所有选择的最小值
for (int coin : coins) {
// 子问题无解,跳过
if (i - coin < 0) {
continue;
}
dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
}
}
return (dp[amount] == amount + 1) ? -1 : dp[amount];
}Note
为啥
dp数组中的值都初始化为amount + 1呢,因为凑成amount金额的硬币数最多只可能等于amount(全用 1 元面值的硬币),所以初始化为amount + 1就相当于初始化为正无穷,便于后续取最小值。为啥不直接初始化为 int 型的最大值Integer.MAX_VALUE呢?因为后面有dp[i - coin] + 1,这就会导致整型溢出。